Introduction
The auto trade has all the time been on the forefront of innovation, continuously searching for methods to enhance effectivity, security, and buyer satisfaction.
Predictive modeling provides a brand new dimension to this effort by enabling data-driven selections that profit producers, insurers, and shoppers.
On this mission, we deal with predicting normalised losses for automobiles, a vital metric for assessing vehicle threat and figuring out insurance coverage premiums.
Normalised losses are standardised metric that quantifies the relative threat of a automobile incurring insurance coverage losses.
This text leverages numerous machine studying fashions to offer correct and actionable predictions.
Car insurance coverage dataset
Normalised losses are sometimes calculated primarily based on sure necessary knowledge similar to historic claims knowledge, adjusted to account for various elements similar to restore prices, automobile options, and accident frequency.
This enables for constant comparability throughout completely different automobile fashions.
The dataset contains 206 rows and 26 columns, providing complete insights into numerous automobiles. It consists of technical specs, insurance coverage threat rankings, and normalised loss values, offering a strong basis for evaluation.
To entry the dataset please go to the next hyperlink, which incorporates an in-depth article detailing a previous exploratory evaluation performed on the car dataset.
Intention of predictive modelling
On this mission, we purpose to foretell normalised losses utilizing numerous machine studying fashions, together with Linear Regression, Ridge Regression, ElasticNet, Random Forest, Gradient Boosting, and Help Vector Machines (SVM).
The principle steps to realize this purpose embody:
- Information Preprocessing
- Mannequin Choice
- Mannequin Analysis
- Hyperparameter tuning
- Characteristic Significance
Information Preprocessing
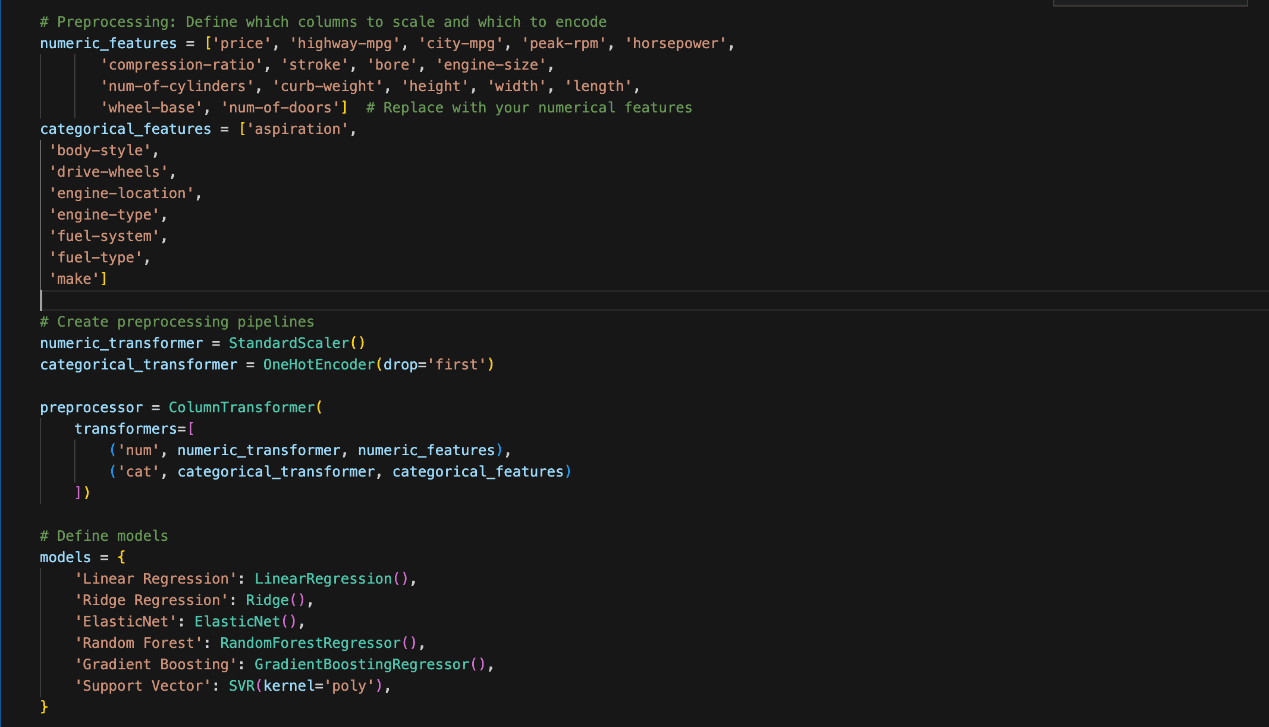
Preprocessing is important for making ready the dataset earlier than making use of machine studying fashions. The Python coding within the determine beneath was used.
The options had been divided into two classes, particularly Numeric and Categorical.
The numeric options embody values similar to ‘value’, ‘horsepower’, and ‘engine-size’. We scaled them utilizing StandardScaler to make sure all numeric variables have the identical weight when fed into the fashions.
Alternatively, the explicit or non-numeric options embody ‘aspiration’, ‘body-style’, and ‘fuel-type’.
Categorical knowledge was reworked utilizing OneHotEncoder, which converts them into binary columns with 1 representing the presence and 0 representing the absence of every class.
Mannequin Choice
A number of algorithms will be utilised within the prediction of normalised losses within the vehicle insurance coverage enterprise.
Nevertheless, the efficiency of those algorithms will range relying on the character of the dataset and the precise downside to be tackled.
Due to this fact, you will need to check out a number of algorithms and evaluate them primarily based on sure analysis standards to pick out the most effective one whereas additionally aiming to steadiness complexity and interpretability.
Under are the algorithms thought-about and explored.
1. Linear Regression
Linear Regression is among the easiest machine studying fashions. It tries to discover a straight line (or hyperplane) that most closely fits the information.
The thought is that the goal variable ‘y’ (like ’normalised-loss’`) will be expressed as a linear mixture of the enter options ‘x’ (like’`value’,’`horsepower’, and so on.). Study extra about Linear Regression right here.
The purpose of Linear Regression is to minimise the error between the expected and precise values. The error is measured utilizing the imply squared error (MSE).
2. Ridge Regression
Ridge Regression is like Linear Regression however with a penalty for giant coefficients (weights). This helps forestall overfitting.
Math is sort of the identical as Linear Regression, however it provides a regularisation time period that penalises giant weights.
Study extra about Ridge Regression right here.
3. Random Forest Regressor
Random Forest is an ensemble methodology that mixes a number of Choice Timber. A call tree splits the information into smaller teams, studying easy guidelines (like “if value > 10,000, predict excessive loss”).
A Random Forest builds many determination bushes and averages their outcomes. The randomness comes from:
– Deciding on a random subset of information for every tree.
– Utilizing random subsets of options at every cut up.
Every tree makes its personal prediction, and the ultimate result’s the common of all tree predictions.
Vital ideas:
– Splitting Standards: In regression, bushes are normally cut up by minimising the imply squared error (MSE).
– Bagging: This implies every tree is skilled on a random subset of the information, which makes the forest extra sturdy.
Extra about Random Forest right here.
4. Gradient Boosting Regressor
Gradient Boosting is one other ensemble methodology that builds determination bushes. Nevertheless, in contrast to Random Forest, every tree learns from the errors of the earlier one. It really works by becoming bushes sequentially.
The primary tree makes predictions, and the following tree focuses on correcting the errors made by the earlier tree.
Study Gradient Boosting Regressor right here.
5. Help Vector Regressor (SVR)
Help Vector Regressor tries to discover a line (or hyperplane) that most closely fits the information, however as a substitute of minimising the error for all factors, it permits a margin of error. SVR makes use of a boundary the place it doesn’t care about errors (a margin).
SVR tries to steadiness minimising errors and maintaining the mannequin easy by solely adjusting predictions exterior this margin.
6. ElasticNet
ElasticNet combines the concepts of Lasso Regression and Ridge Regression. Like Ridge, it penalises giant coefficients but in addition like Lasso, it might cut back some coefficients to zero, making it helpful for characteristic choice.
ElasticNet is sweet when you will have many options and wish each regularisation and have choice.
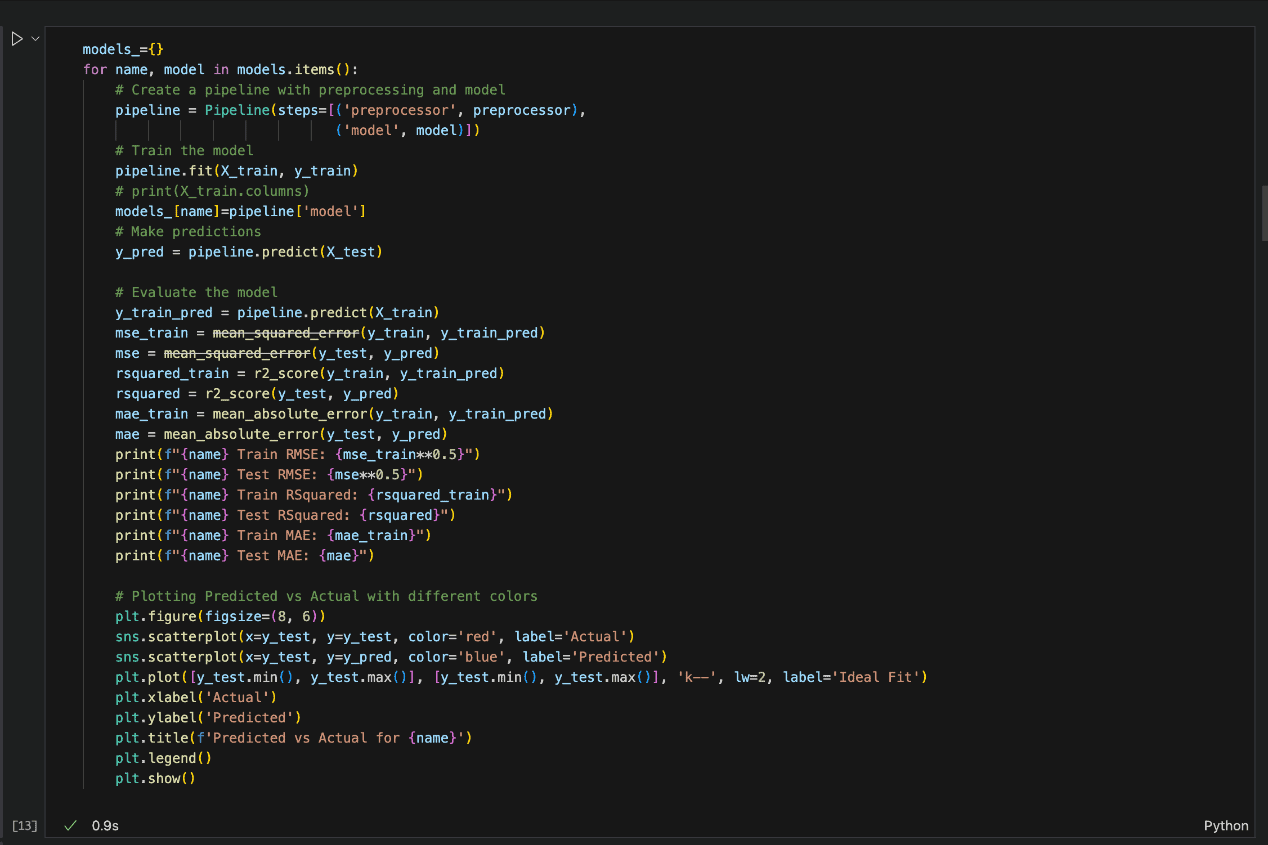
Mannequin Analysis
A number of the extra generally identified mannequin analysis strategies or metrics used on this mission are RMSE, MSE, and R-squared.
Splitting the dataset into coaching and check units is an analysis methodology used earlier than the primary mannequin is even constructed.
By setting apart a portion of the information because the check set, we be sure that the mannequin is evaluated on unseen knowledge, offering an early and unbiased estimate of how effectively the mannequin will generalise new knowledge.
After experimenting with completely different algorithms utilizing the check cut up ratio, the next efficiency metrics had been used to match the regression fashions on an equal footing:
Imply Squared Error (MSE):
MSE measures the typical squared distinction between the precise and predicted values.
A decrease MSE signifies a greater match, however it’s delicate to outliers.
Root Imply Squared Error (RMSE):
The RMSE is the sq. root of MSE, and it’s helpful as a result of it’s in the identical items because the goal variable.
Imply Absolute Error (MAE):
MAE measures the typical absolute distinction between the precise and predicted values.
It’s much less delicate to outliers than MSE.
R-squared (R²):
R² explains how a lot of the variance within the goal variable is captured by the mannequin.
The next R² (nearer to 1) signifies a greater match, however it’s not all the time dependable for small datasets.
Within the snapshot of the Python code beneath, every of the mannequin algorithm and the analysis methodology is carried out.
Outcomes
The next desk summarises the outcomes of the completely different fashions used primarily based on RMSE, MAE, and R-squared values:
|
Fashions |
RMSE |
MAE |
R-squared |
|
Linear Regression |
16.4 |
13.9 |
80.5 |
|
Ridge Regression |
23.4 |
17.7 |
60.3 |
|
Random Forest Regressor |
26.8 |
18.4 |
48.2 |
|
Gradient Boosting Regressor |
23.5 |
15.1 |
60.0 |
|
Help Vector Regressor |
36.7 |
33.9 |
2.8 |
|
Elastic Web |
28.7 |
25.6 |
40.4 |
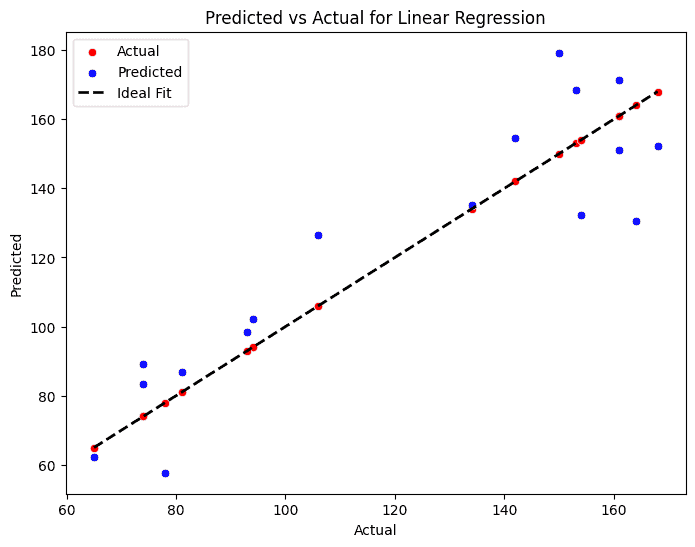
From the outcomes introduced, Linear Regression appears to display the most effective general efficiency in comparison with the opposite fashions, adopted by Gradient Boosting Regressor and Random Forest.
Nevertheless, it might be noticed that the tree-based fashions (Random Forest and Gradient Boosting Regressor) could also be exhibiting indicators of overfitting.
Whereas their coaching efficiency is close to good, their check efficiency is considerably worse, indicating that these fashions could not generalize effectively to unseen knowledge.
|
Fashions |
RMSE practice |
RMSE check |
MAE practice |
MAE check |
R-Squared practice |
R-Squared check |
|
Random Forest Regressor |
6.9 |
26.8 |
4.3 |
18.4 |
96.1 |
48.2 |
|
Gradient Boosting Regressor |
4.1 |
23.5 |
3.1 |
15.1 |
98.6 |
60.0 |
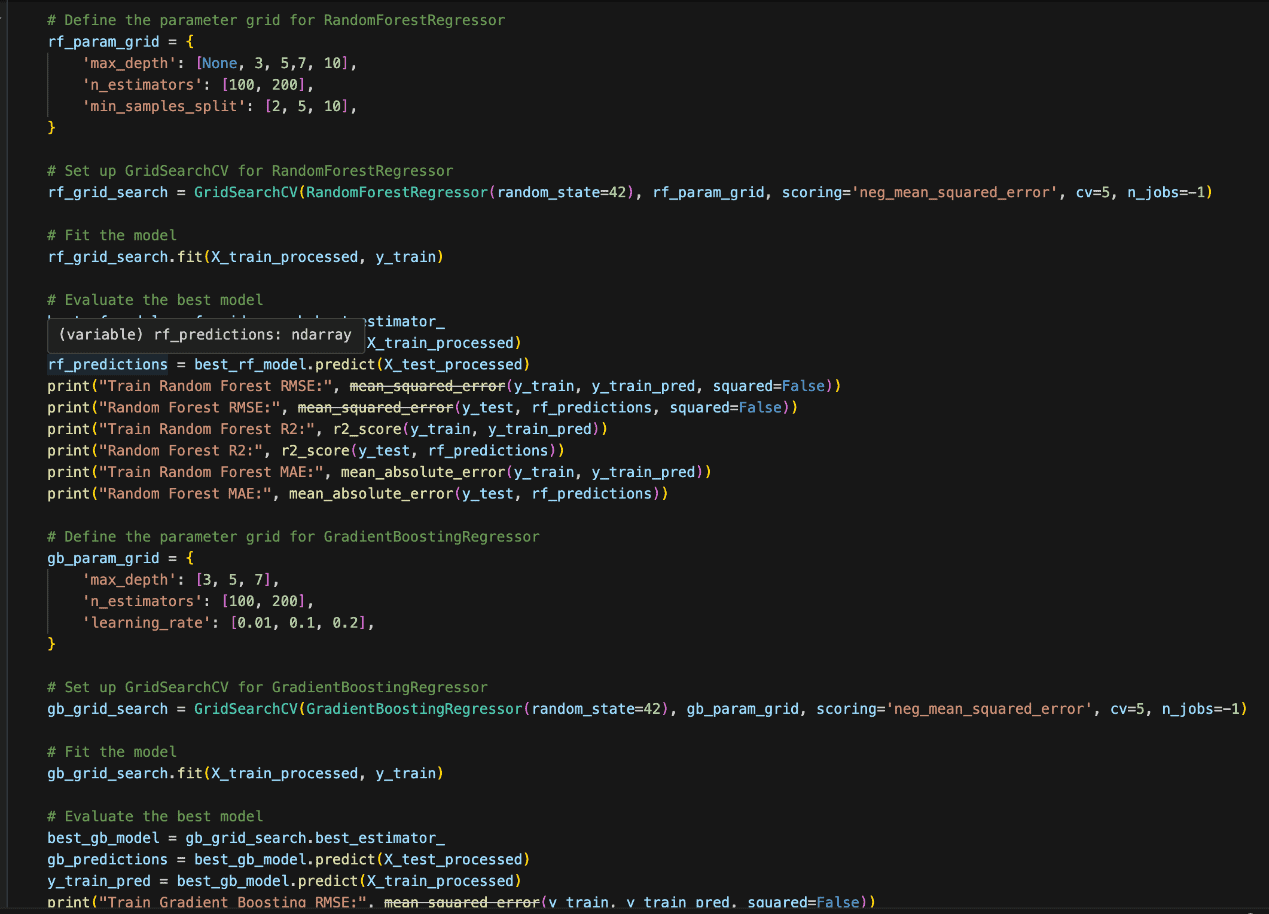
Hyperparameter Tuning
Selecting the best hyperparameters can considerably enhance the mannequin’s efficiency and its means to generalise to unseen knowledge. If the hyperparameters are usually not tuned accurately:
- The mannequin would possibly overfit (carry out effectively on coaching knowledge however poorly on check knowledge).
- The mannequin would possibly underfit (fail to seize the patterns within the knowledge).
Carry out Hyperparameter Tuning
- Handbook Search: You manually strive completely different mixtures of hyperparameters and consider efficiency. This method will be time-consuming and inefficient.
- Grid Search: You outline a set of hyperparameter values to strive, and the algorithm tries each mixture. It’s exhaustive however computationally costly, particularly when the search area is giant.
Since we’ve got a comparatively small pattern dimension, we will likely be utilizing grid search as seen within the Python code snippet beneath:
Outcomes after tuning
|
Fashions |
RMSE practice |
RMSE check |
MAE practice |
MAE check |
R-Squared practice |
R-Squared check |
|
Random Forest Regressor |
8 |
25.2 |
5.7 |
19.3 |
94.8 |
54.1 |
|
Gradient Boosting Regressor |
5.1 |
21.9 |
3.8 |
15.2 |
97.9 |
65.8 |
Although the coaching scores for the tree-based fashions have decreased and the check scores have improved, the hole between the 2 nonetheless signifies indicators of overfitting.
This means that, regardless of the changes, the fashions wrestle to generalise.
Total, Linear Regression stays the top-performing mannequin, exhibiting no indicators of overfitting and delivering sturdy, balanced outcomes throughout each coaching and check datasets.
Characteristic Significance
To additional improve the interpretability of your mannequin, it’s important to grasp which options contribute essentially the most to the ultimate predictions.
The strategy for evaluating characteristic significance varies by mannequin sort. For tree-based fashions like Random Forest or Gradient Boosting, we might utilise the built-in characteristic significance methodology.
For Linear Regression, the mannequin’s coefficients will be analysed. Bigger absolute values point out options which have essentially the most vital impression on the mannequin’s predictions.
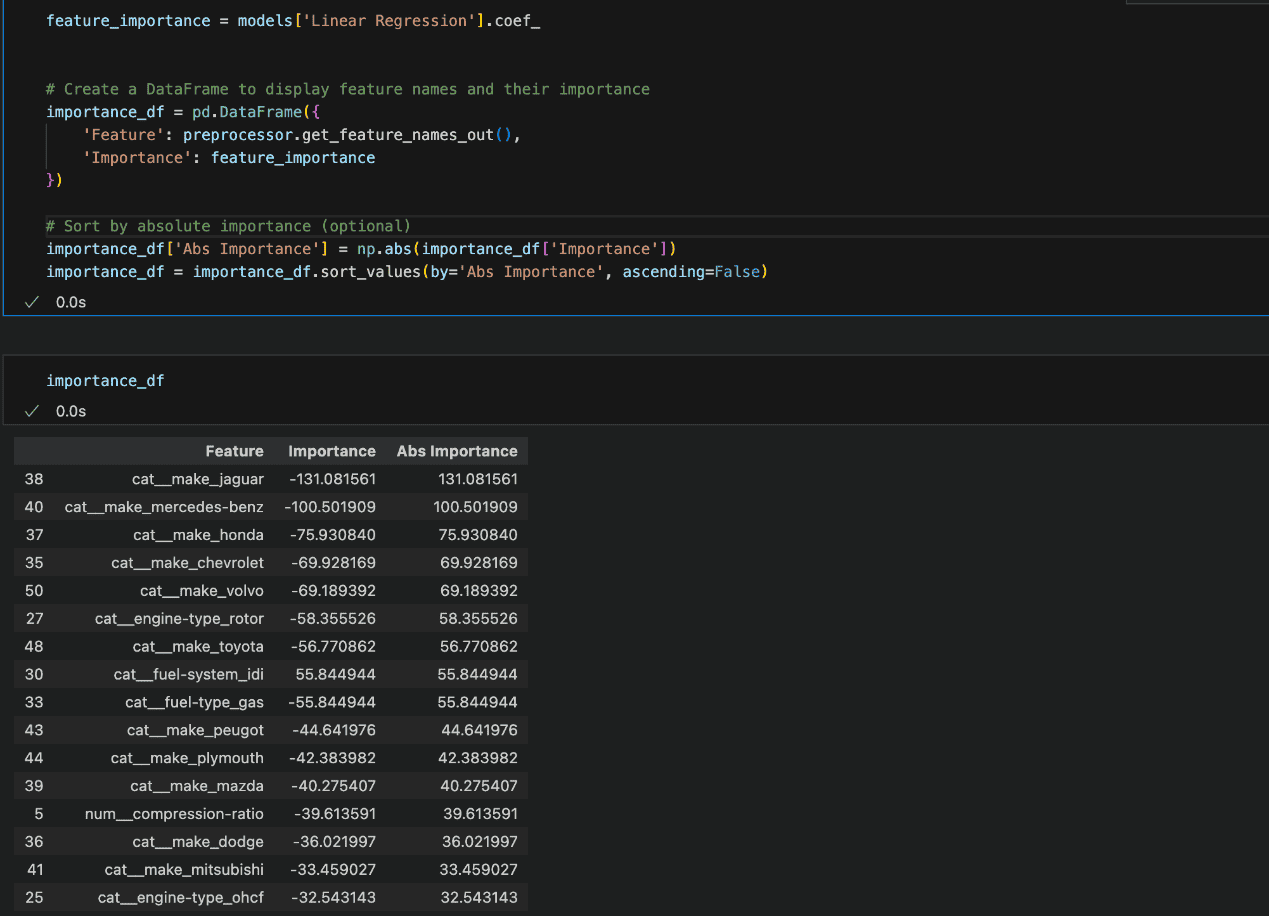
The characteristic significance reveals that the classes reworked into options by means of one-hot encoding have the most important coefficients.
This means that these categorical variables, as soon as cut up into binary columns, have a big affect on the mannequin’s predictions.
It’s frequent in such circumstances for sure classes inside a characteristic to hold extra weight, particularly in the event that they symbolize distinct patterns or behaviors that strongly impression the result.
Nevertheless, it’s necessary to fastidiously interpret these outcomes, as giant coefficients don’t essentially imply the characteristic is inherently necessary—simply that it has a stronger relationship with the goal within the given mannequin.
Mannequin Interpretability utilizing SHAP
One other methodology of calculating characteristic significance is by utilizing SHAP.
SHAP (SHapley Additive exPlanations) is a strong characteristic significance software that makes use of cooperative recreation principle to assign every characteristic an significance worth primarily based on its contribution to a mannequin’s predictions.
By computing Shapley values, SHAP quantifies how a lot every characteristic influences the output for particular person predictions, enabling a transparent understanding of mannequin habits.
To calculate characteristic significance utilizing SHAP, this methodology will be adopted:

The SHAP plot displayed beneath exhibits the significance of various options on the mannequin’s predictions. The SHAP values on the x-axis point out the extent to which every characteristic influences the mannequin’s output, with constructive or damaging contributions.
The additional the SHAP worth is from zero, the stronger the characteristic’s impression on the prediction. The colours symbolize the characteristic values: blue for low values and pink for prime values.
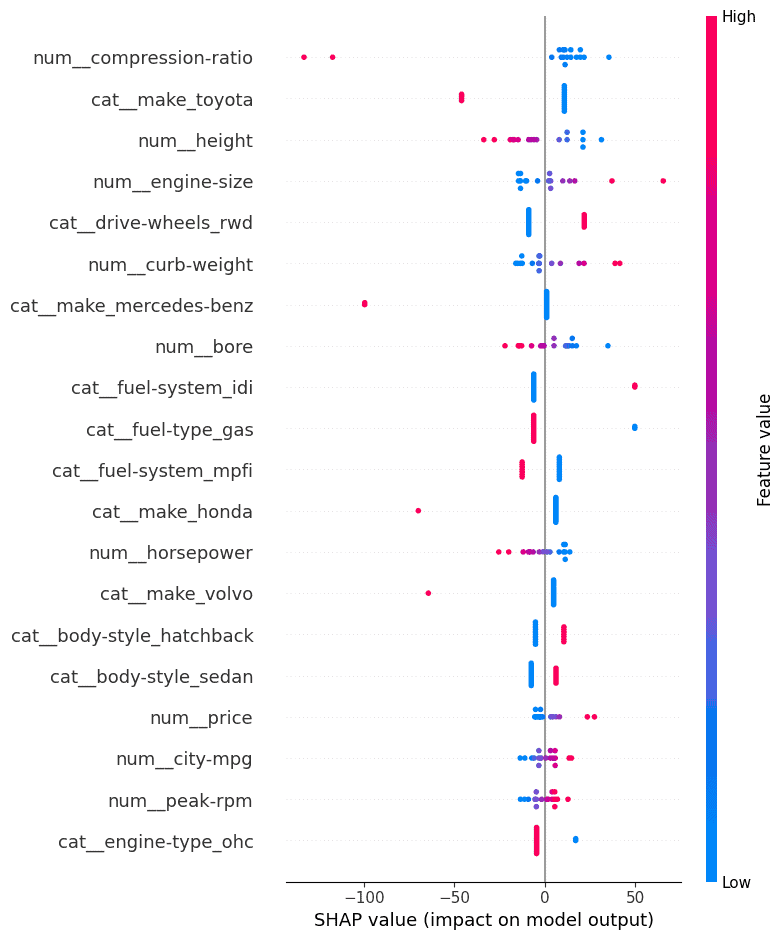
Key Observations:
- Compression-ratio (num__compression-ratio) has essentially the most vital impression, with greater values (in pink) rising the SHAP values and positively influencing the mannequin’s predictions. Conversely, decrease compression ratios (in blue) push the prediction within the damaging course.
- Make Toyota (cat__make_toyota) additionally has a powerful affect. Excessive SHAP values counsel that automobiles of this make contribute positively to the mannequin’s consequence.
- Top (num__height) exhibits a transparent pattern the place greater values contribute positively, and decrease values push predictions downward.
- Engine dimension (num__engine-size) and curb weight (num__curb-weight) are among the many prime options, with bigger engines and heavier automobiles typically contributing to greater predictions. This aligns with expectations, as these attributes usually correlate with automobile efficiency.
- Make Mercedes-Benz (cat__make_mercedes-benz) have a definite impact, with greater SHAP values driving the prediction positively, reflecting its luxurious standing.
- The drive wheels (cat__drive-wheels_rwd) characteristic, notably rear-wheel drive automobiles, are inclined to affect predictions positively when rear-wheel drive is current.
- This SHAP evaluation reveals that a few of the most influential options are associated to automobile specs (engine dimension, curb weight, top) and particular automobile make (Toyota, Mercedes-Benz).
Enterprise implications of automobile insurance coverage threat prediction outcomes
- Insurance coverage Premium Calculation: By predicting normalized losses, insurance coverage firms can extra precisely set premiums for various automobile fashions. Automobiles with greater predicted normalized losses can be thought-about riskier, resulting in greater premiums, and vice versa.
- Danger Evaluation for New Automobile Fashions: Automobile producers or sellers might use this mannequin to evaluate the insurance coverage threat score of recent or upcoming automobile fashions. This helps in evaluating how dangerous it could be to insure the automobile primarily based on its options and the historical past of comparable automobiles.
- Accident/Declare Danger Prediction: Predicting normalised losses might point out how inclined a automobile is to accidents or harm primarily based on options like engine dimension, horsepower, or physique sort, permitting producers or shoppers to evaluate the chance of incurring future restore prices.
- Automobile Score Methods: Predicting normalized losses can contribute to a extra complete automobile score system for patrons, serving to them make knowledgeable selections in regards to the long-term prices of proudly owning a specific automobile, together with insurance coverage bills.
Wrapping up
In abstract, this mission demonstrates the facility of predictive modeling in estimating normalised losses for automobiles.
Among the many fashions examined, Linear Regression emerged as the highest performer, placing an efficient steadiness between accuracy and ease.
Superior fashions like Random Forest and Gradient Boosting, whereas promising, exhibited challenges with overfitting, underscoring the significance of cautious mannequin tuning and analysis.
The evaluation additionally highlighted the important options influencing predictions, similar to engine dimension, curb weight, and particular automobile make, offering actionable insights for stakeholders.
By leveraging these fashions, insurance coverage firms can optimise premium pricing, producers can assess threat rankings for brand new fashions, and shoppers could make extra knowledgeable automobile buy selections.
This method exemplifies how machine studying can bridge the hole between complicated knowledge and sensible, real-world functions.














